Category: Computer Science

Simple Elliptic Curve Cryptography in Python compatible with seccure

Instead of RSA, you can use an Elliptic Curve algorithm for public/private key cryptography. The main advantage is that keys are a lot smaller. With RSA you need keyservers to distribute public keys. With Elliptic Curves, you can just write: my public key is *jMVCU^[QC&q*v_8C1ZAFBAgD.

There are two drawbacks: first, Elliptic Curve cryptography is even harder to understand than plain RSA and secondly, there are only a few implementation of Elliptic Curve cryptography. In fact: I did not find any maintained Elliptic Curve package for Python.

Thus I wrote a Python package compatible with the excellent commandline utility seccure written by Poettering. Here are some examples of how to use the original commandline seccure and how to do the same thing in Python.

For a private key, you just pick a (long!) password. You can derive the public key with seccure as follows:

$ seccure-key
Assuming curve p160.
Enter private key: my private key
The public key is: 8W;>i^H0qi|J&$coR5MFpR*Vn

In Python

>>> import seccure
>>> str(seccure.passphrase_to_pubkey(b'my private key'))
'8W;>i^H0qi|J&$coR5MFpR*Vn'

Now, to encrypt a message for the public key:

$ seccure-encrypt -o private.msg '8W;>i^H0qi|J&$coR5MFpR*Vn'
Assuming MAC length of 80 bits.
Go ahead and type your message ...
This is a very secret message!
^D

In Python:

>>> ciphertext = seccure.encrypt(b'This is a very secret message\n', b'8W;>i^H0qi|J&$coR5MFpR*Vn')
>>> ciphertext
'\x00\x146\x17\xe9\xc1\x1a\x7fkX\xec\xa0n,h…

To decrypt the encrypted message:

$ seccure-decrypt -i private.msg
Assuming MAC length of 80 bits.
Assuming curve p160.
Enter private key: my private key
This is a very secret message!
Integrity check successful, message unforged!

In Python:

>>> seccure.decrypt(ciphertext, b'my private key')
'This is a very secret message\n'

To create a signature

$ seccure-sign
Assuming curve p160.
Enter private key: my private key
Go ahead and type your message ...
This message will be signed
^D
Signature: $HPI?t(I*1vAYsl$|%21WXND=6Br*[>k(OR9B!GOwHqL0s+3Uq

In Python:

>>> seccure.sign(b'This message will be signed\n', b'my private key')
'$HPI?t(I*1vAYsl$|%21WXND=6Br*[>k(OR9B!GOwHqL0s+3Uq'

And to verify a signature:

$ seccure-verify '8W;>i^H0qi|J&$coR5MFpR*Vn' '$HPI?t(I*1vAYsl$|%21WXND=6Br*[>k(OR9B!GOwHqL0s+3Uq'
Go ahead and type your message ...
This message will be signed
^D
Signature successfully verified!

In Python:

>>> seccure.verify(b'This message will be signed\n', b'$HPI?t(I*1vAYsl$|%21WXND=6Br*[>k(OR9B!GOwHqL0s+3Uq', b'8W;>i^H0qi|J&$coR5MFpR*Vn')
True

You can find the Python library on Github.

Update: added support for Python 2.6, 2.7, 3.2 and 3.3.

GStreamer: accurate duration

When decoding, for instance, a variable-bitrate MP3, gstreamer reported durations are, to say the least, estimates. I’ve tried to get a better result in a few ways. First off, some files yield a duration tag, but even if you’re lucky and it is there, there are no guaranties about precision. After that I tried seeking to the end (GST_SEEK_END) of the stream and querying the position, which gstreamer didn’t like. Finally, routing the audio into a fakesink, waiting for the end of stream and then querying for the position gives the right result. It’s not the prettiest method, but it works.

This is a Python script that prints the duration of a media to stdout.

The Cuckoo Hashtable

A Hashtable algorithm is a specific algorithm to implement key-value pair datastructure with efficient by-key look-ups using hashing of the keys. A hashtable contains a list of buckets. In a simple implementation, the i-th bucket, contains the key-value pairs in a list of which the key has a hash that is i modulo the amount of buckets. The hash-table would increase the amount of buckets if any bucket contains more than a fixed amount of pairs. This results in a constant-time look-up, but an insertion might invoke a expensive rebuild.

There are a few variations on Hash Tables. I’d like to share a really smart one: the Cuckoo Hashtable.

The Cuckoo hashtable expects two different hash-functions for the keys. Instead of storing a list of pairs in each bucket, the Cuckoo Hash table stores a single pair in each bucket. When inserting a pair, it is inserted in one of the two possible locations. If it happens to be occupied, the old pair is replaced. Then the replaced pair is inserted at its other possible location, potentially kicking out another pair. This step is repeated, until there is no displaced pair or a loop is detected. When a loop is detected, the hash-functions can be changed, if the buckets are for the most part empty -or- when the table is almost full, the amount of buckets can be increased. It can be shown that an insertion has a amortized constant time. (The buckets can be resized in-place, and each entry is repositioned as if it was displaced by another.)

If I’d own a botnet… (1)

…and didn’t want to loose it if my control servers got shut down, I’d let every orphaned zombie randomly connect to hosts in a given IP range, and challenge them to give a preimage of a hardcoded hash. [ detail: add a salt to prevent replay attacks ]. With a sufficiently safe casu quo large range, it also might be helpfull to allow zombies to forward still orphan zombies.

git‘s versus svn‘s storage efficiency

At Codeyard we maintain a git and a subversion repository (which are synced with each other) for each of the >115 projects. The following graph shows the repositories plotted logarithmically according to the size of their whole server side subversion repository horizontally and their git repository size vertically:

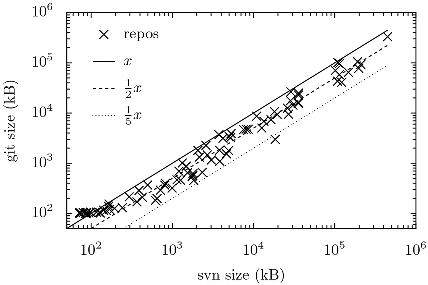
To make more sense of the logarithmic nature of the graph, I’ve added three lines. The first (solid black) indicates the points of which both sizes are equal. The second course dashed line indicates the points of which the subversion repository is twice as large as the git repository. And lastly, the third finely dashed line indicates the points of which the subversion repository is five times as large as the git repository.

All projects for which git is less storage efficient, are smaller than 100Kb. The projects for which git is most storage efficient (up to even 6 times for a certain C# project), are all of medium size (10–100MB) and code-heavy. For the other projects, which are blob heavy (eg. images), git and subversion are close (git beats svn by ~20%).

One notable disadvantage of huge (someone committed a livecd image) git repositories, is an apparent [tex]\geq2N[/tex] memory usage of git repack even if I tell it not to with --window-memory.

Linux 2.6.24-bw-r34

Again an update for my bw-tree. There isn’t a tree that includes reiser4 and TuxOnIce without a lot of other bloat, so I created one myself.

Download the big diff or the seperate patches broken out.

Note I pulled in new patches for reiser4 from the -mm tree against -rc8 which should fix the Reiser4 flush problem a bit.

Update Patched against 2.6.24 stable. New TuxOnIce patched added and the genpatches. Please note that I haven’t tested Reiser4 thoroughly enough on this version.

CaCert.org

CaCert is a Certification Authority that works with a web of trust: people meet and assure (similar to keysigning) eachother. If you’ve been assured by enough people you’ll be able to let your ssl server key be certified by cacert. It’s a lot more secure than other CA’s who just give anyone a certificate who pays enough.

Still a hierarchical system with a CA is flawed. When the CA is compromised, the whole system fails. PGP’s web of trust hasn’t got this weakness.

(Got a nice shiny cacert certified ssl certificate on my webserver now)

Stupid PHP (1) (Strings are faster than Arrays)

When I slowly build a big string out of little bits, the worst thing to do in most languages is to just use string concatenation:

for(something) {
 str .= little_bit;
}

Why? Everytime a little bit is added to str, there must be a new string allocated big enough to contain str and the new little bit. Then the actual str must be copied in. In most languages there are constructs to efficiently build strings like this instead of concatenating. StringBuffer in C#. StringIO in Python.

But no, PHP has to be stupid. There is no nice construct and you’ll end up using concatenation. So, I thought to be smart and make use of PHP array’s and implode. Arrays are here for having elements added and removed all the time so they are properly buffered and should be great at having lots of small elements added. And when I want to pack it all into one big string, I can use PHP’s builtin implode function.

I wanted to try it out and created two scripts: a.php concats a little (10byte) string one million times and b.php appends it to an array and then implodes it. And because I’m also interested in the performance of implode I got a script c.php that’s identical to b.php but doesn’t implode afterwards. These are the results:

a.php (concat) 0.320s
b.php (array append and implode) 0.814s
c.php (array append) 0.732s

Indeed, string concatenation with all its allocation and copying is actually faster than plain simple array appending. PHP is stupid.

The (or at least a better) Solution to Spam

There is no easy way to distinguish between a human and a spambot. It’s an arms race which we’ll always be behind. I’m talking here about spam in more general—not only on e-mail but also on for instance Wikipedia or on blogposts. Even if we would have a perfect-solution to test whether there is a human behind something, we still have to combat cheap labour in India: real people spamming “by hand”.

I think the solution is a Web of Trust similar to that of PGP. An identity (not necessarily a person) publishes who she trusts (not to be spammy/phishy) or not trusts. Ideally everyone would be in one big web. Only someone who my blog via-via trusts may post.

Obviously one still may gather trust of people over time and enter the web of trust and then start spamming with that identity. However, then that identity will be marked untrusted by people and also the people who initially marked the identity as trusted will be less trusted. Also, there are way more sophisticated measures of establishment in the web/trust to conceive than just being trusted via-via by one identity.

There is no way to prevent spam perfectly, but the amount of work that has to go in to making an identity trusted and established in the web is several orders of magnitude greater than any other protection we have. The big problem: we don’t have such an ubiquitous web of trust yet. (Yes, it’ll be in SINP if I’ll get around to working on it)

linux 2.6.22-bw-r1

There isn’t a tree that contains reiser4, suspend2 and the gentoo patches — so I created one. This revision adds the -stable patches and the new gentoo patches.

One big patch: bw-r1-for-2.6.22.diff.bz2
Patches broken out: bw-r1-for-2.6.22.tar.bz2

To apply the one big patch, use: bzcat bw-r1-for-2.6.22.diff.bz2 | patch -p1 inside a vanilla 2.6.22.

Online Cycle Detection in Directed Graphs

A short while ago I came across a quite interesting problem. Design a datastructure (and algorithms) to maintain a Directed Acyclic Graph.

There has to be only one operation: adding a link between two given nodes. This operation must be able to detect and deny any new link that would cause a cycle. For simplicity, nodes are identified by sequential ids starting with 0.

An example:

addLink 0, 1 -> True
addLink 1, 2 -> True
addLink 2, 0 -> False # Fails because it would create a cycle

addLink 0, 1 -> True
addLink 1, 2 -> True
addLink 0, 2 -> True # This isn't a real cycle, so it's perfectly fine

It’s rather trivial to create a [tex]\mathcal{O}\left(n+\ell\right)[/tex] (where [tex]n[/tex] is the number of nodes and [tex]\ell[/tex] the number of links). I conjecture there exists a [tex]\mathcal{O}\left(\log n\right)[/tex] algorithm.