Finaly I got grip of a recording of an electric guitar without distortion and applied the gamma wave distortion on it:
Tag: guitar
Gamma Wave Effect
As promised a few pictures of the electric guitar effects we’re working on,
first up, the gamma wave effect.
The gamma wave effect pulls the amplitudo’s either to the 0 line or the -1/1 line, just like the gamma on your monitor does:

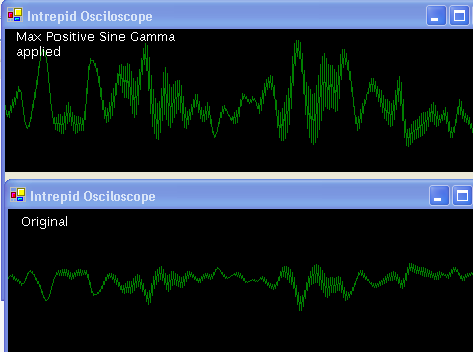
The effect basicly makes the wave a lot louder and gets rid of the faint sounds. When on fully applied as in the images above it also creates some distortions due to either making the wave unharmonic-ish or getting rid of the nuances.
Another image taken on a higher oscilation (smaller zoom):
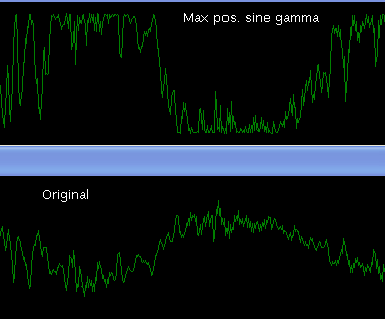
This clearly shows the distortion
(The inversion of peak and valley doesn’t matter for for sound only the transition from a valley to a peak matters)
Electric Guitar Distortion
As I said before I am working with some others on a software based distortion. I finaly got the base running pretty smoothly but the main obstacle is how to create that distortion electric guitars use.
We came up with about 3 different methods:
(When I got my osciloscope control working I’ll take before and after pictures, for now I ain’t sure how the formula’s effect real-world sound yet)
Gamma corrections
This works a bit like the gamma of your monitor. The input for graph for gamma correction is called the epsilon which comes in 2 forms, linear and sine. The first one creates a more distortion like sound than the latter but also makes the wave not harmonic anymore which possible means that most of the distortion like sound is caused by the speakers not handling unharmonic waves very well. The latter one only sounds near the amplitudo distorted.
Sharpening valleys/tops
This method requires some buffering of the current top (or valley) of the wave and sharpenes it by a specific amount. This works a bit like the gamma correction method although it works on every volume making it usefull too for low-volume sounds. The major problem is that it requires tracking a top or a valley, which with a high bitrate requires a really big buffer to analyze, and it has a delay of one top/valley. The big problem is that this isn’t ideal for live playing for which it was designed, a delay of a few extra hundreds of a second would be noticable and it is fairly possible that this algorithm requires too much resources.
Adjusting speed resistance
At a certain point in a wave you can derive the speed and the angle. By registering the original speed and resistance of the wave a derived one can be created which could leed to sharper or softer edges of a top/valley just as the previous method but without being required to analyze the whole top/valley. We’re hoping this method will work best but this is just a concept hoping to work out as it should.
If anyone actually knows how analog distortions work exactly we would be more than happy to learn about it, just comment.
More on this to come…
Working on a software based distortion for the electric guitar
At the moment I am busy creating a software based distortion for an electric guitar.
The most challenging part is getting effects to work, to explain this in more detail you need to know how a computer handles audio.
Sound itself is nothing more than a vibration in the air. It can be represented by the amount of force the air is pushing or pulling.
A tone of a specific frequency would look like:
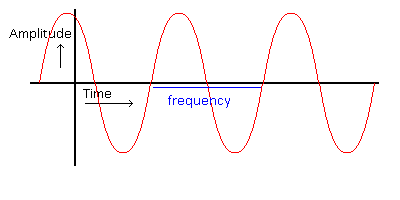
A computer stores sound by sampling the amplitude of the air at regular interfals.
It would be easy to write a program to increase the frequency of the sound above, but a normal sound doesn’t look that regular:
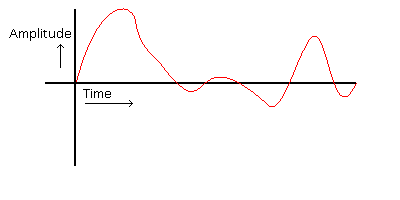
Increasing the bass or treble of that wave would require some advanced algorithms, which take time to execute which creates a larger delay. One thing that a distortion shouldn’t do is lag.
More on this when some stuff is working.